Computability Theory, Nonstandard Analysis, and their connections (arxiv link)

​

The strength of compactness in Computability Theory and Nonstandard Analysis  (APAL, arxiv link)

​

Dag Normann and Sam Sanders

​

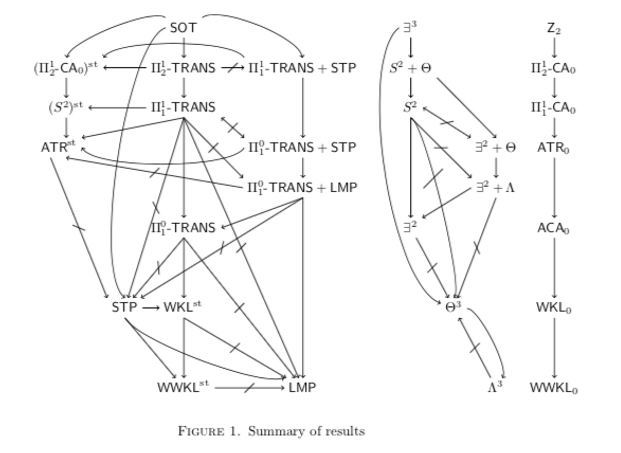
The aim of these two papers is to explore the connection between computability theory and Nonstandard Analysis (NSA hereafter).  We show that Robinson's nonstandard compactness from NSA translates to a realiser for Heine-Borel compactness for uncountable covers, and visa versa.  The former for the unit interval is called STP, while the realiser is called the special fan functional     .  Weak counterparts, called LMP and the functional   , are also defined.  Figure 1 below desribes how these functionals interact with known comprehension functionals.  Note that (non)-implications on the left-hand side are obtained using (non)-implications on the right-hand side side. 

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

We emphasise that many of these results where first obtained using NSA.  In particular, the surprising behaviour of the special fan functional (and hence Heine-Borel compactness; see here) was first conjectured based on the fact that in NSA, the axioms Transfer and Standardisation are independent, and the same holds for fragments.

​

​

​

​